I Don't Trust Auto-Shufflers

Legal Disclaimer (please don’t sue me)

The following is an analysis of what a casino (if acting maliciously) could do using automatic shuffling machines in order to gain an unfair advantage towards their patrons. I am not accusing, alleging, nor implying that any casino is in fact doing this.

Motivation

I recently went on a trip to Las Vegas. Obviously, I’m going to (responsibly) gamble a little bit while I am there. Personally, my game of choice is BlackJack. It actually requires enough thinking to be interesting and if played perfectly is the only game at the casino that is theoretically beatable.

The key phrase there is in theory. While perusing tables at various Vegas casinos, pretty much every game with a reasonable rule set (e.g. blackjack pays $3{:}2$, DAS, etc) and low enough stakes (I’m not trying to bet \(\$50\) a hand) used an automatic shuffling machine. Being a cynical software engineer, I didn’t trust these things for a second.

In this post, I will show how a casino could maliciously utilize automatic shuffling machines in order to gain an unfair advantage. I am not accusing, alleging, nor implying that any casino is in fact doing this.

How Do Automatic Shuffling Machines Work?

From my recent trip, I observed $2$ types of automatic shuffling machines. The first type I will call a Random Shuffle Machine (RSM). These take all the cards being used and shuffles them together. Then, the dealer takes out all the shuffled cards, has a player cut the cards, and places them inside the shoe. Then the cards are dealt until the shoe runs out of cards. The second type is called a Continuous Shuffle Machine (CSM). This machine provides cards to the dealer one at a time. After each hand, the dealer puts the cards back into the machine, and these cards are redistributed back into the shoe. Hence, the name “continuous”, since the shoe never ends. You can see an example here of how these could work (although note that this is a very old machine).

We would like to believe RSMs and CSMs are operating fairly. In theory, cards could be placed into these machines in a randomized initial order, and the machine randomly permutes them. Since the initial order was random and the permutations were random, then the output will also be random. While these do exist, they are not what is being used in casinos.

There are two key additional features of auto-shufflers used in casinos. First, they scan every card put into the machine. Modern casino cards have invisible readers, which let the machine know what card it is. This is why most casinos no longer sell used cards (a fact I learned on my recent trip). Second, the cards are not shuffled by randomly permuting them. Instead, the deck order is generated in software and the automatic shuffler precisely places the cards in this order. If after learning this, you believe automatic shufflers are fairly shuffling the cards…I know a Nigerian prince who would like to speak with you.

The only question that remains is, how can this technology be used maliciously?

Beating the Casino in BlackJack

Before we can create malicious shuffling algorithms, we must first understand how players get an edge over the casino. If you want to learn the rules of BlackJack and the basics of card counting, I recommend these videos [1, 2]. The main thing to know is that $10$, $J$, $Q$, $K$, and $A$ are all good cards. Players gain an advantage when these high-valued cards are disproportionately clumped together at the end of a shoe (this is because you are more likely to get dealt a $21$, which pays $3{:}2$). On the other hand, if the cards are mostly evenly distributed (especially at the end of a shoe), then the casino has the largest advantage.

Basic Strategy refers to the mathematically optimal way to play each hand of BlackJack. Given your cards and the card being shown by the dealer (the dealer’s upcard), there is a table that tells you exactly what to do [3]. Unfortunately, Basic Strategy is not enough to beat the casino. With perfect Basic Strategy, the casino has a \(0.5\%\) advantage, meaning over the long run you are expected to lose \(\$0.50\) for every \(\$100\) you bet.

Card Counting is a method of keeping track of how many high-valued cards have come out. If you reach the end of the shoe and you know that very few high-valued cards have appeared, then the few remaining cards must contain them. Therefore, it is now dramatically more likely that the next card is a high card. Therefore, you have an advantage and you should bet more, as it’s much more likely you are going to win. Also, the mathematically optimal decision changes with the count, but I won’t get into that [4, 5, 6]. With perfect play, card counting can give you an advantage of \(1\%\) over the casino, meaning over the long run you are expected to make \(\$1\) for every \(\$100\) you bet.

Malicious Shuffling Algorithms

Now that we know the conditions card counters are looking for, we will develop some algorithms to prevent or mitigate those conditions. In particular, we want to prevent card counters from knowing when there is a disproportionately large clump of high-valued cards.

Malicious CSM Algorithm

This type of shuffling machine completely destroys card counting by design since there is no concept of a running count. Since cards are redistributed back into the shoe after each hand, seeing a lot of low-valued cards does not make it more likely you’ll see high-valued cards next hand. Effectively, each hand of independent.

I model a CSM by simply reshuffling the shoe after each hand.

Malicious RSM Algorithm

This type of shuffling machine is much more interesting. Once the final order is produced, the RSM can no longer influence the cards. Moreover, unlike CSM’s, these shoes are countable, meaning the current hand depends on the previous hands. Our job in constructing a malicious algorithm is to prevent card counters from gaining an advantage despite knowing the count.

We cannot achieve this by advantageously pre-arranging the cards since they are cut by one of the players. Therefore, the first card of our pre-arrangement will go somewhere in the middle. For example, if you construct a shoe with a very low count, and then randomly cut the shoe, about half the time it will result in a shoe with a very high count. I experimented with various malicious pre-arrangements and found no reliable methods.

Instead, our strategy is to ensure the high-valued cards ($10$, $J$, $Q$, $K$, and $A$) are evenly distributed throughout the entire shoe. This will ensure the running count is never too high, and therefore card counters cannot gain an advantage. Consider the following pythonic pseudocode.

def shuffle_cards(cards, number_of_groups):
    # Step 1
    high_cards, low_cards = separate_high_cards_from_low_cards()
    random.shuffle(high_cards)
    random.shuffle(low_cards)

    # Step 2
    grouped_high_cards = group_cards(high_cards, number_of_groups)
    grouped_low_cards = group_cards(low_cards, number_of_groups)

    # Step 3
    grouped_cards = merge_groups(grouped_high_cards, grouped_low_cards)
    for group in grouped_cards:
        random.shuffle(group)
    
    # Step 4
    return flatten(grouped_cards)

Let’s unpack this. We’ll do a very simple example with $13$ cards (one of each) and $2$ groups. In Step $1$ we separate the high-valued cards from the low-valued cards.

In Step $2$ we make $2$ groups of high-valued cards and $2$ groups of low-valued cards.

In Step $3$, we merge these groups together.

Finally, in Step $4$, we just flatten this $2\text{D}$ array.

Notice that we have this parameter number_of_groups, which lets us tune exactly how malicious we want the RSM to be. A larger number of groups means more evenly distributed which is less advantageous to a card counter.

Simulating the Algorithms

In order to test the effectiveness of my malicious shuffling algorithms, I created a Monte Carlo simulation for BlackJack in Python. You can find the code on my GitHub here.

Simulation Parameters

I am using the following Table Rules

• Dealer stands on all $17$s
• Double after split is allowed
• Late surrender is allowed
• BlackJacks pay $3{:}2$

I neglect some aspects of the game such as insurance and even money. I also do not put a restriction on the number of splits allowed in a single hand. I also let players continue their action after splitting aces.

The Basic Strategy player always flat bets. I’ve set this to \(\$10\) for easy maths. The Card Counting player uses a very simple bet spread (there are more profitable ones, but this is often used as a baseline).

For example, if the true count \(\text{True Count} = \frac{ \text{Running Count} }{ \text{Number of Decks Remaining in the Shoe} }\) is $+4$, and the base bet amount is \(\$10\), then the card counter will bet \(4 \times \$10 = \$40\).

Baseline - Fair Shuffling

First, let’s see what happens if the cards are shuffling fairly. The following is the result of simulating $1$ million hands for both Basic Strategy and optimal Card Counting.

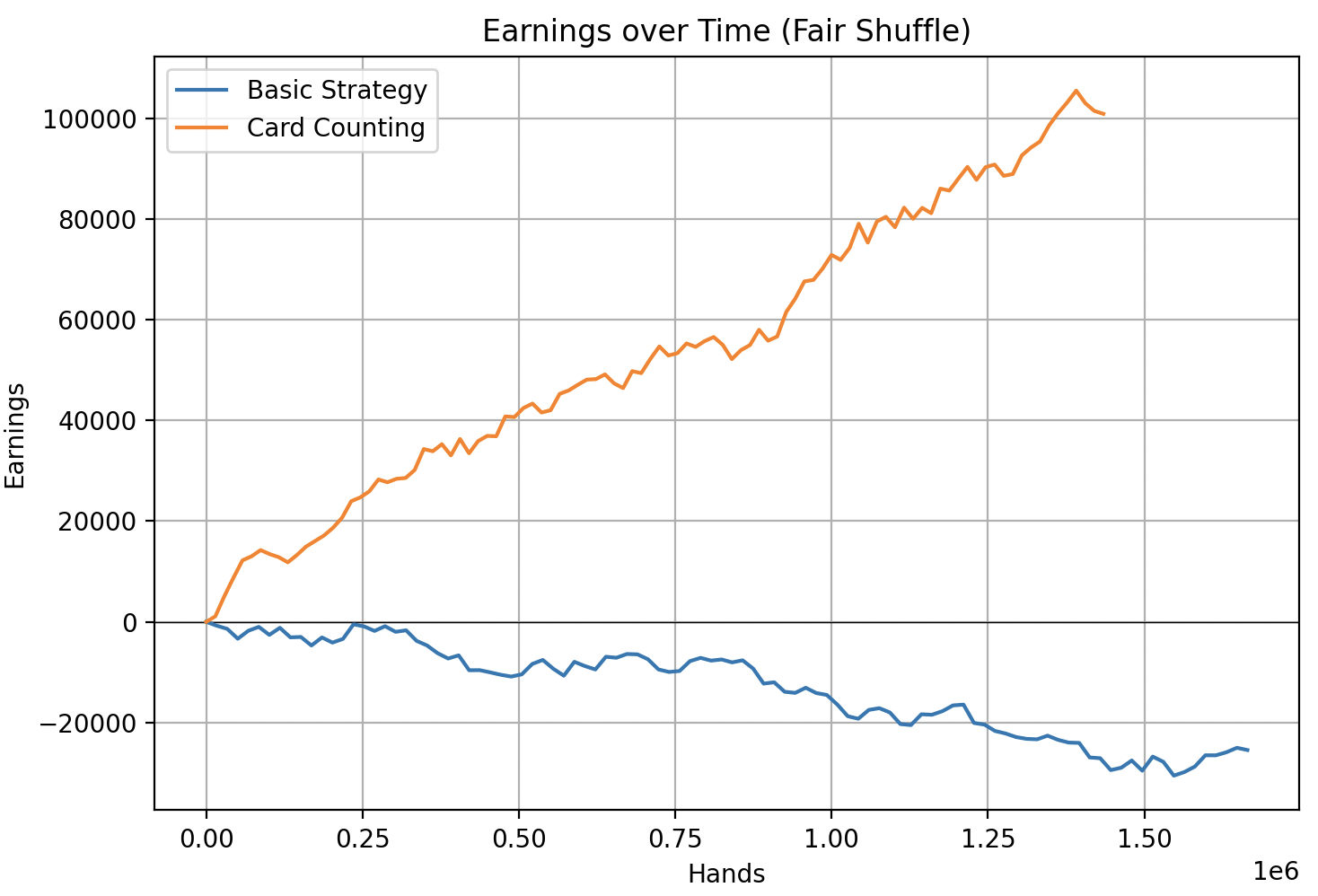
We see exactly what we expected. Over the long run, Basic Strategy is losing but only slightly, and Card Counting provides the player with a significant advantage.

Malicious CSM Algorithm

Now let’s see the effects of a CSM.

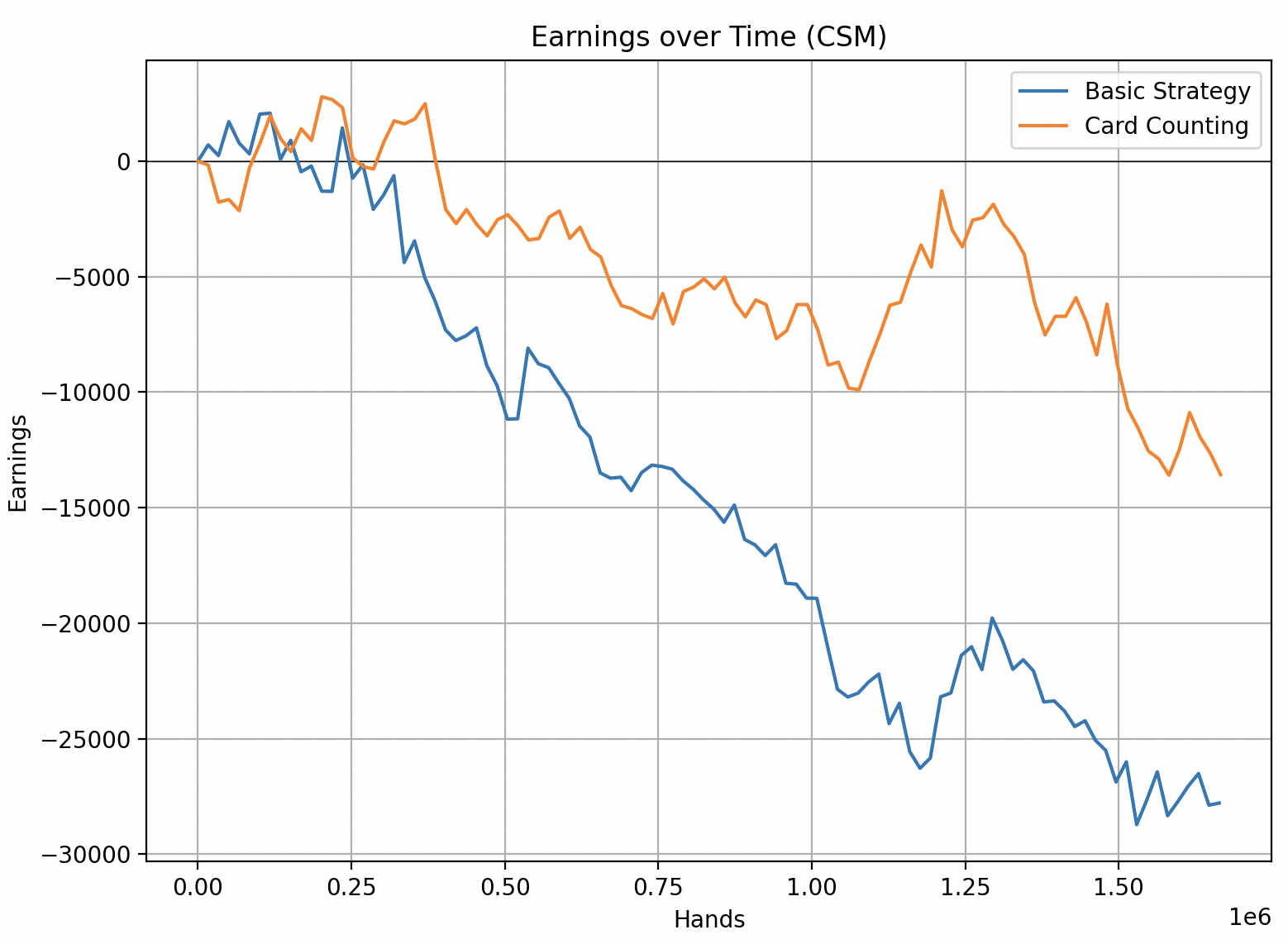
To be honest, this wasn’t as losing as I expected, but it’s still not great. I think this graph shows a pretty realistic representation of what you get with CSM’s (speaking anecdotally).

An interesting thing to notice is how much the variance of the game increased compared to the fair shuffle. I’m not sure why it should be the case. If you have any ideas, please let me know.

Malicious RSM Algorithm

The RSM algorithm is interesting because we can fine-tune it using the number_of_groups parameter. Below I show two simulations. The first is for number_of_groups = 40 ($2$ high-valued cards per group). The second is for number_of_groups = 25 (about $3$ high-valued cards per group).

  

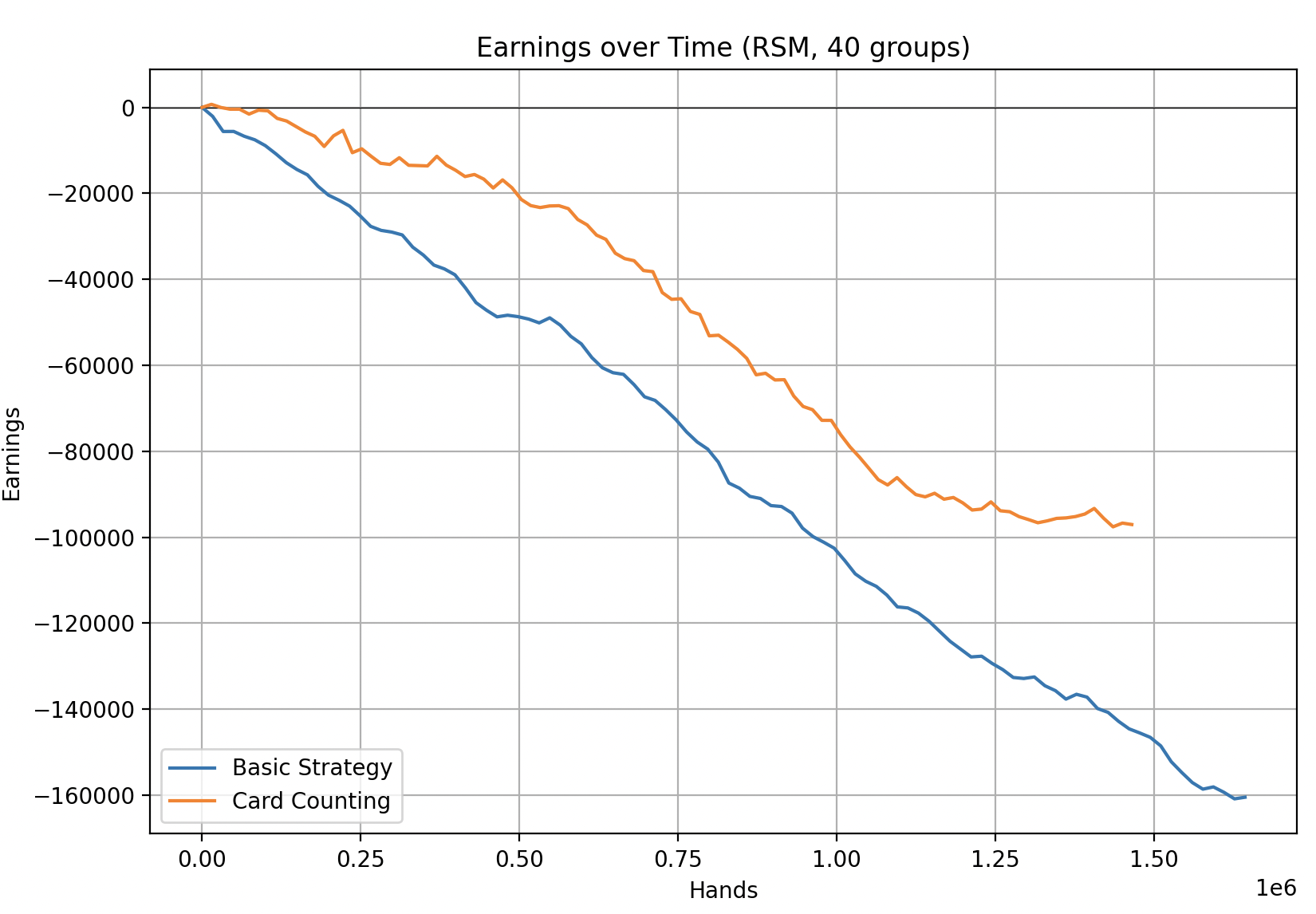
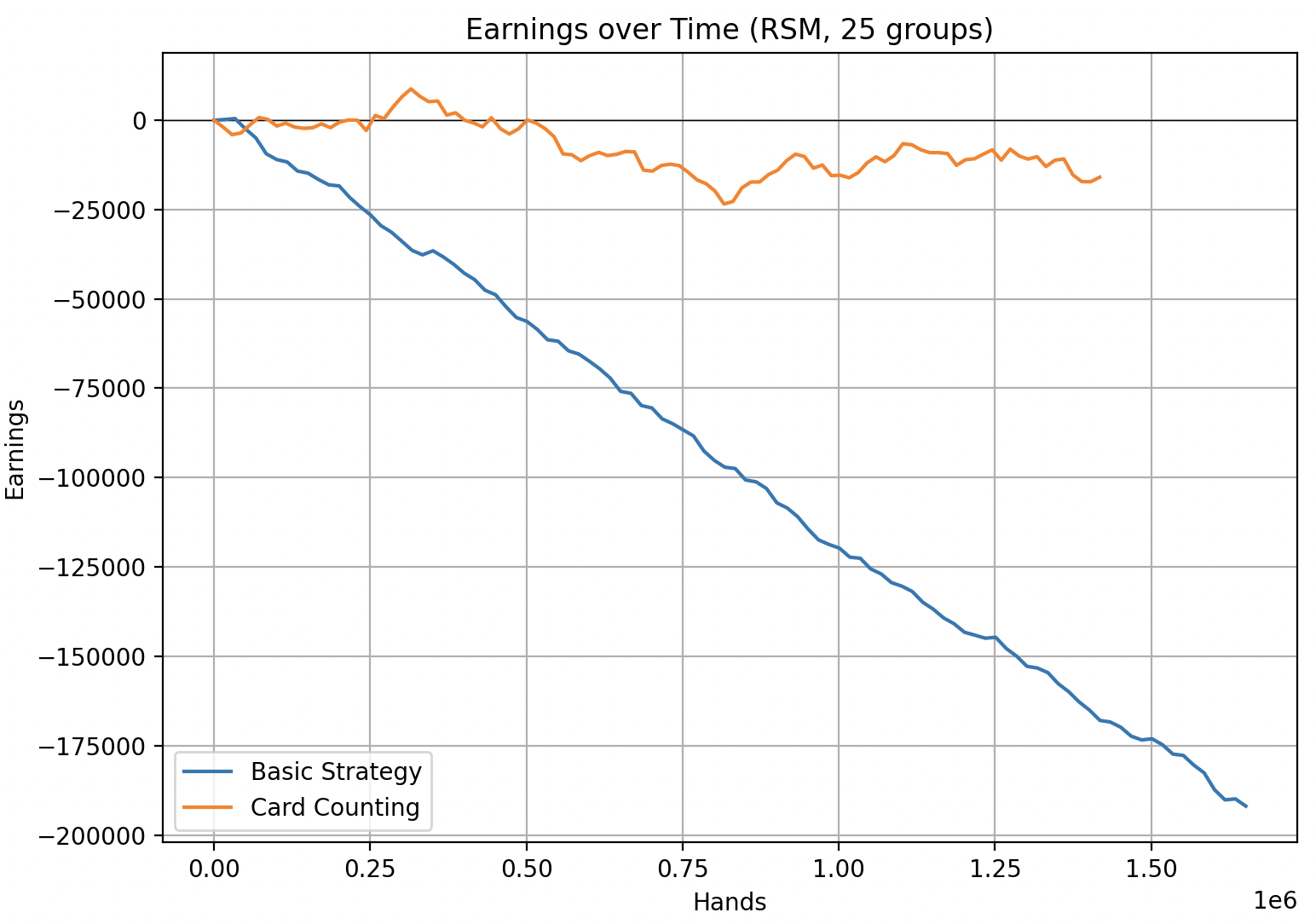
I was shocked at how effective this malicious shuffling algorithm was. The RSM $40$ group simulation is ridiculous for both card counters and basic strategy players. While the $25$ group simulation hovers around even for card counters, it’s still incredibly losing for basic strategy players. This algorithm is so losing that there’s no way casinos actually use it because people would notice.

Conclusion

In this post, I demonstrated how much of an influence the shuffle can have over a game of BlackJack. On a personal level, I wanted to justify why I do not trust automatic shuffling machines. While I do not think casinos are utilizing the RSM algorithm I proposed (as it’s far too losing for the player), for all we know they could be manipulating the cards to their advantage using more subtle algorithms. When money is involved, never underestimate what people will do.

My recommendation, just stick to hand shuffling and avoid all of this madness. Or just don’t gamble.