How Many Unique Racks are There?
Introduction
In North America the most popular billiard games are 8-ball, 9-ball, and 10-ball. To begin each of these games, balls are arranged into a rack according to certain rules. In this post, I will analyze the number of unique starting racks in each of these games, according to the WPA and UPA official rules.
9-Ball
The WPA and UPA have different racking rules for 9-ball, I will analyze each.
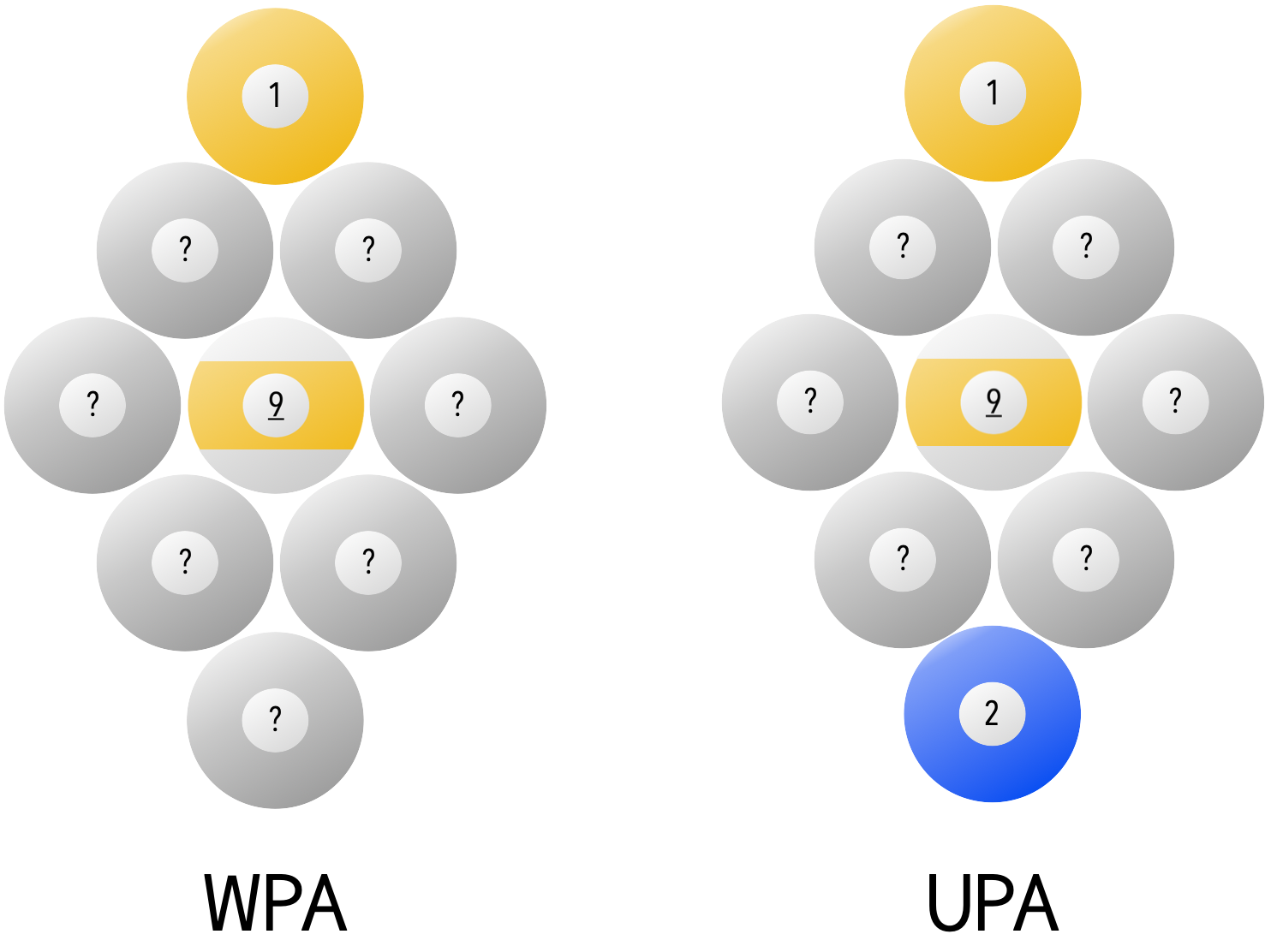
WPA
According to Section 5.2 of the WPA official rules as of Sep 15, 2025, the $1$ ball is placed at the top, the $9$ ball in the middle, and all other balls placed randomly.
This means we need to determine the number of ways to arrange 7 balls. There are 7 choices for the first ball, 6 choices for the second ball, 5 choices for the third ball, etc. This means the total number of combinations is
\[7! = 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 5040\]Therefore, there are $5040$ unique racks of 9-ball according to WPA rules.
UPA
According to the official UPA 9-ball rules at the time of writing, they have an additional restriction that the $2$-ball must be placed at the bottom of the rack.
Now, the number of combinations is the number of ways to arrange 6 balls, which is
\[6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 840\]Therefore, there are $840$ unique racks of 9-ball according to WPA rules.
10-Ball
The WPA and UPA have different racking rules for 10-ball, I will analyze each.
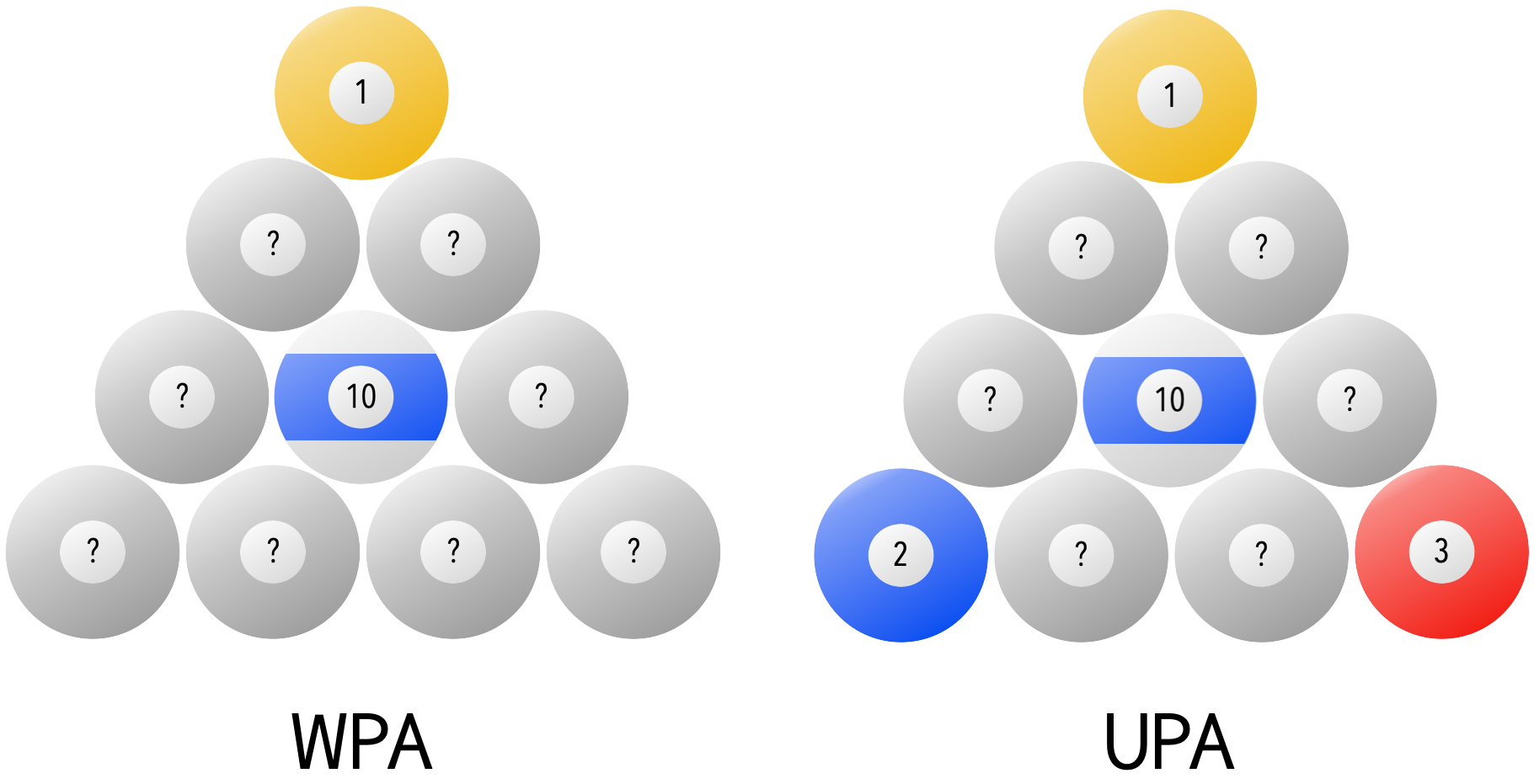
WPA
According Section 6.2 of the WPA official rules as of Sep 15, 2025, the $1$ ball is placed at the top, the $10$ ball in the middle, and all other balls placed randomly.
Therefore, by the exact same argument as before, there are $8! = 40,320$ unique racks of 10-ball.
UPA
According to the official UPA 10-ball rules at the time of writing, they have an additional restriction that the $2$-ball and $3$-ball must be placed at the bottom corners (in either order).
There are $6!$ ways to choose the positions of the 6 random balls, and $2$ ways to choose the position of the $2$ and $3$ ball.
Therefore, there are $2 \times 6! = 1440$ unique racks of 10-ball according to the UPA rules.
8-Ball
The WPA and the UPA both agree on the racking rules.
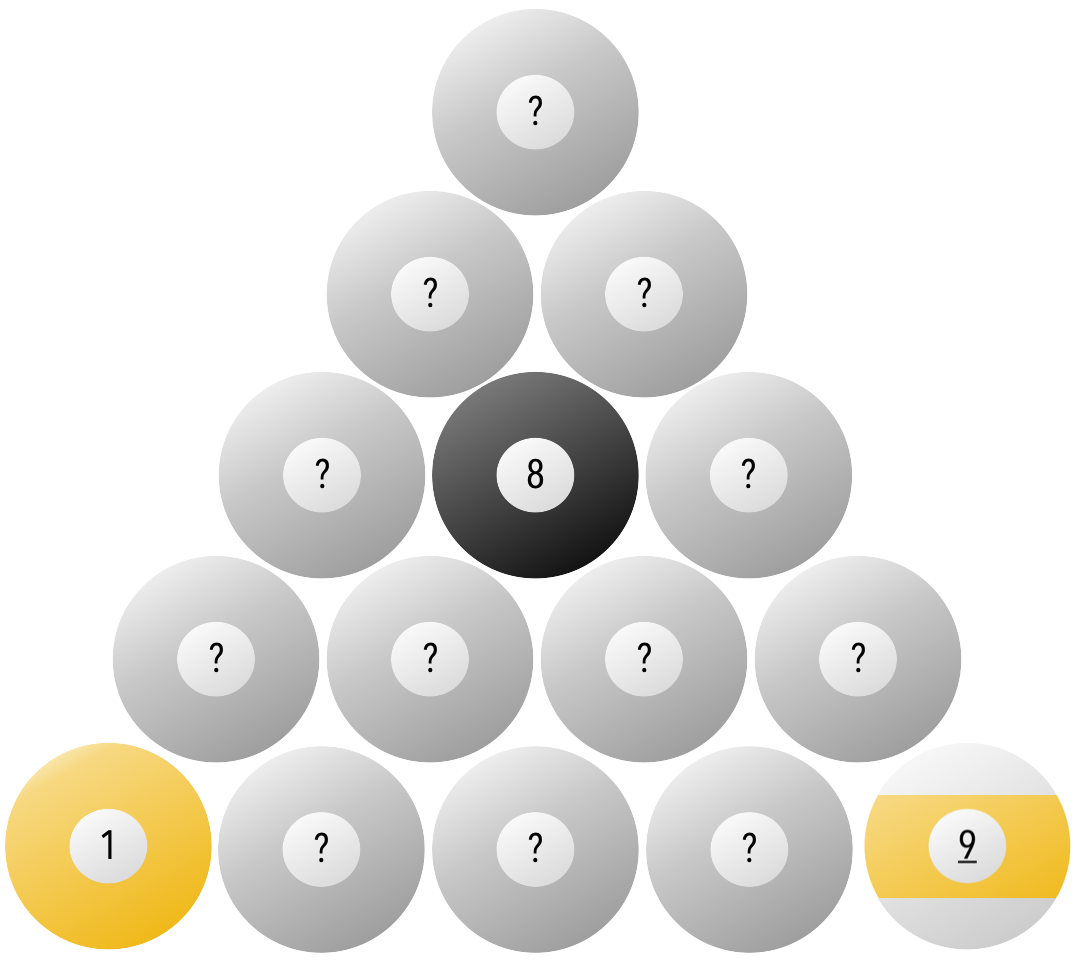
The analysis is a bit more complicated, so first we need to define some terms.
Definitions and Rules
In 8-ball, there are three types of balls:
- seven solids
- seven stripes
- one $8$ ball.
Two balls are of the same parody if they are either both solids or both stripes.
A valid rack of 8-ball consists of placing the $8$ ball is placed in the middle, bottom left and right corners are different parodies, and all other balls placed randomly
When defining a unique rack of 8-ball, there are two important considerations.
- Every solid ball is indistinguishable from every other solid ball. The numbers and colors don’t mean anything in 8-ball
- Every striped ball is indistinguishable from every other striped ball. The numbers and colors don’t mean anything in 8-ball
- Interchanging solids and strips does not result in a unique rack
Consider the following examples
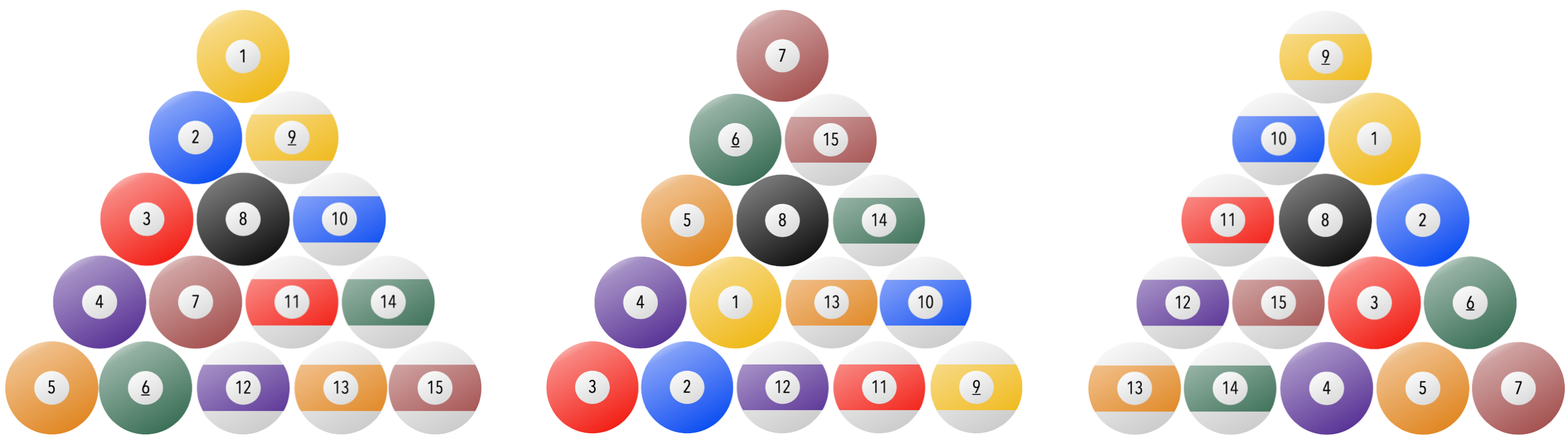
All of these racks will be considered the “same” when we are counting unique racks. Between the first two racks I have just permuted the order of the solid and stripes. Between the first and third rack I have interchanged the positions of solids and stripes.
Analysis
First, let’s assume that the bottom left corner is a solid and the bottom right corner is a stripe. This does two things at once. First, it will ensure that all the racks in our analysis are valid racks. Second, it accounts for parody between solids and stripes by fixing one orientation.
Now we just have to pick the arrangement of the rest of the 6 solids and 6 stripes. Really, we just have to pick the spots for the solids, and all of the remaining spots are forced to be stripes.
There is 12 available spots for the first solid, then 11 available for the second solid, then 10 available for the third solid, etc. However, each solid is interchangeable, so we have to divide by the number of ways to arrange the solids in their chosen spots. Therefore, the number of combinations is
\[\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\]There is a special notation for this
\[\binom{6}{12} = \frac{12!}{6! (12 - 6)!} = 924\]Therefore, there are $924$ unique racks of 8-ball.